Learn you a Haskell for Fun and Profit

....Because trying something new is fun!

What is Haskell?

• Functional - Given the arguments, always returns the same output ie no global or local state.
• Lazy
• Statically typed

Learn you a Haskell

Learn You a Haskell for Great Good the goal of the reading group is to get through this book.

Week 1 is about

• Getting Started
• Lists (and list comprehension)

Getting started

• Download Haskell Minimal x86
• VS Code Text Editor
• Haskell Syntax Highlighting

REPL

Running from Powershell GIT in windows

string1 = "hello"
string2 = "world"
greeting = string1 ++ string2

doubleMe x = x + x

-- 6

b = doubleMe 3

-- 16.6  as + works on ints and floating-point numbers

c = doubleMe 8.3

-- * is an infix function which takes 2 numbers and multiplies (as opposed to a prefix)

a = 49 * 100

-- 10/3 gives 1 as a remainder

s = mod 10 3
-- backtick infix style gives 1 as a remainder

t = 10 `mod` 3

-- Cons operator

-- [3,5,7,11]

favNums = 3:5:7:11:[]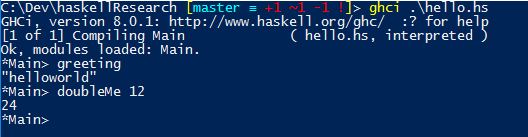

Loading hello.hs and calling functions

• Ctrl D - exit from GHCI in Powershell
• Ctrl L - cls

Euler 1

Project Euler is where I start when learning a new language to flex my new ‘toolbelt’..

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23. Find the sum of all the multiples of 3 or 5 below 1000.

-- 1.  Head of list

a = head [1,2,3]
-- 2,3.  Tail of the list

b = tail [1,2,3]

-- List comprehension (output function is before the pipe)

-- x 'such that', x goes to [1..999]

-- filtering (weeding out lists by predicates)

h = sum [x | x <- [1..999], x `mod` 3 == 0 || x `mod` 5 == 0]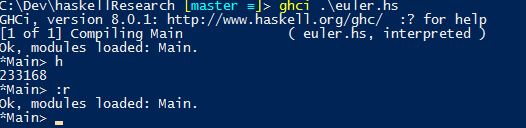

running the function h to get the answer. Reloading changes :r in file euler.hs

Euler 2

-- Each new term in the Fibonacci sequence is generated by adding the previous two terms.

-- By starting with 1 and 2, the first 10 terms will be:

-- 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...

-- By considering the terms in the Fibonacci sequence whose values do not exceed four million, 

-- find the sum of the even-valued terms.


-- [7,9,11,13,15]

sumOfLists = zipWith (+) [1,2,3,4,5] [6,7,8,9,10]

-- zipWith adds 2 lists together

fibs = 1 : 1 : zipWith (+) fibs (tail fibs)

-- [1,1,2,3,5,8,13,21,34,55,89,144,233,377]

q = takeWhile (< 4000000) fibs

--4613732

o = sum [ x | x <- takeWhile (< 4000000) fibs, even x]

Euler 3

The prime factors of 13195 are 5, 7, 13 and 29. What is the largest prime factor of the number 600851475143 ?

-- Euler 3

-- The prime factors of 13195 are 5, 7, 13 and 29.

-- What is the largest prime factor of the number 600851475143 ?


-- number is prime if only divisible by 1 and itself

-- https://stackoverflow.com/a/5811176/26086

-- eg if checking isPrime 12

-- 3 * 4 are factors

-- 2 * 6 are factors..

-- one of the factors has to be less than the sqrt

-- and if there is a factor, then it isn't a prime

-- only need check up to the sqrt of number to see if it can be divided with remainder of 0


-- getting the square root as an int

-- x 35 = 5

-- x 144 = 12

x num = floor (sqrt (fromIntegral num))

-- If result set is empty isPrime = True

isPrime num = [x | x <- [2..floor (sqrt (fromIntegral num))], num `mod` x == 0] == []

-- The factors of a number 

facs num =  [x | x <- [3..num], num `mod` x  == 0]
-- [5,7,13,29,35,65,91,145,203,377,455,1015,1885,2639,13195]

q = facs 13195

-- Prime factors

facs' num =  [x | x <- [3..num], num `mod` x  == 0, isPrime x]
-- [5,7,13,29]

q' = facs' 13195

-- Problem is that it doesn't stop after giving the correct answer

-- as its checking all the way up to 600851475143 to see if its a factor

-- [71,839,1471,6857]

r = facs' 600851475143

-- only need to check up to sqrt of 600851475143 to see if it's a factor and a prime

facs'' num =  [x | x <- [3..floor(sqrt (fromIntegral num))], num `mod` x  == 0, isPrime x]
s = facs'' 600851475143

Euler 4

-- Euler 4

-- A palindromic number reads the same both ways. 

-- The largest palindrome made from the product of two 2-digit numbers is 9009 = 91 × 99.

-- Find the largest palindrome made from the product of two 3-digit numbers.


-- [4,3,2,1]

u = reverse [1,2,3,4]

-- int to string

v = show 345
-- string to int

w = read "345" :: Int

-- can reverse the string (as it is a list of chars really)

u' = reverse "1234"
z = reverse v

-- 9009

t = maximum [x*y | x <- [10..99], y <- [10..99], isPalindrome (x*y)]
-- int to string, reverse int to string ie compare 2 strings

isPalindrome num = show num == reverse (show num) 

-- 906609

t' = maximum [x*y | x <- [100..999], y <- [100..999], isPalindrome (x*y)]

_ and Tuples

-- implementing own version of length (of a list)

-- _ means we don't care what we draw from the list.

-- replace every element of a list with 1, then sum

length' xs = sum [1 | _ <- xs] 

-- 4

o = length' [1,2,3,4]

-- Tuple can contain several types

-- returns first component of the Tuple

-- 8

p = fst (8,11) 
-- "Wow"

q = fst ("Wow", False)

-- Which right triangle that has integers for all sides and all sides equal to or 

-- smaller than 10 has a perimeter of 24?

-- a^2 + b^2 = c^2

-- eg 3,4,5 triangle.. perimeter = 12

-- 9 + 16 = 25


-- generate numbers for all sides returning a Tuple

-- [(6,8,10),(8,6,10)]

r = [(a,b,c) | a <- [1..10], b <- [1..10], c <- [1..10], a^2 + b^2 == c^2, a+b+c==24]

Summary of Book so far

Have been able to solve most of the first 9 Euler problems with just list comprehensions.

-- List comprehension (output function is before the pipe)

-- filtering (weeding out lists by predicates)

a = [x*2 | x <- [1..10], odd x, x > 3]

There are a ton of interesting functions in the language!

BrightonFunctionalReadingGroup

Meetup

Highlights from this meeting were

• no let needed in REPL now
• brackets around (+) mean passing + as an argument (actually an infix function to add 2 numbers)

-- zipWith f [a,b,c] [x,y,z]

-- [7,9,11,13,15]

sumOfLists = zipWith (+) [1,2,3,4,5] [6,7,8,9,10]

• ’ is for single characters, “ is for strings (list of chars!)

aa = 'x'
ab = "this is a string"
ac = length ab

• such that, is drawn from

-- x such that, x is drawn from 1 to 10

-- filter by odd x's and x>3 

a = [x | x <- [1..10], odd x, x > 3]

Noel Markham’s exercises link

-- Question 1

-- last element in a list

-- 4

ad = last [1,2,3,4]
-- returns everything except the last element

-- [1,2,3]

ae = init [1,2,3,4]

-- Find the penultimate element in list l

penultimate l = last (init l)


-- Question 2

-- determine if list l is a palindrome

-- palindrome is the same forward as reversed


-- l is a list of characters (a string)

isPalindrome l = l == reverse l
-- True

w = isPalindrome "abba"


-- Question 3

--  Duplicate the elements in list xs, for example "duplicate [1,2,3]" 

--  would give the list [1,1,2,2,3,3]

--  Hint: The "concat [l]" function flattens a list of lists into a single list. 

--  (You can see the function definition by typing ":t concat" into the interpreter. 

--  Perhaps try this with other variables and functions)

--  For example: concat [[1,2,3],[3,4,5]] returns [1,2,3,3,4,5]


-- concat the list of lists into a single list

-- [1,1,2,2,3,3]

ag = concat [[1,1],[2,2],[3,3]]

-- returns a list of lists

-- [[1,1],[2,2],[3,3]]

ai = [[x,x] | x <- [1..3]]

duplicate xs = concat [[x,x] | x <- xs]

--[1,1,2,2,3,3]

ah = duplicate [1,2,3]


-- Question 4

-- Imitate the functionality of zip

-- The function "min x y" returns the lower of values x and y

-- For example "ziplike [1,2,3] ['a', 'b', 'c', 'd']" returns [(1,'a'), (2, 'b'), (3, 'c')]

-- ziplike xs ys = undefined


-- use min to get the number of elements

--ab = min ((length [1,2,3]) length(['a', 'b', 'c', 'd']))


-- returns a list of Tuples with the last 'd' missed off as nothing to match

-- [(1,'a'),(2,'b'),(3,'c')]

aj = zip [1,2,3] ['a', 'b', 'c', 'd']

-- find min length of both lists

xs = [1,2,3]
ys = ['a', 'b', 'c', 'd']
-- 2 (3-1)

ak = min (length xs) (length ys)-1

-- x's at element i, y's at element i, such that i is drawn from 0 to the min length of both lists 

ziplike xs ys = [(xs!!i, ys!!i) | i <- [0..(min (length xs) (length ys)-1)]]



-- DG 1 - Factorials

-- the product of an integer and all the integers below it; e.g. factorial four ( 4! ) is equal to 24.


-- 4*3*2*1 = 24


-- recursion

fac n =
    if n < 2
        -- base case of the recursion.. stop at 1

        then 1
        else n * fac (n-1) 
an = fac 4

-- simplicity

fac' n = product [1..n]

ao = fac' 4

-- works

ap = product [1..4]
aq = product [4,3..1]

-- pattern match?

-- same logic as recursion

fact 1 = 1
fact n = n * fact (n-1)
ar = fact 4

-- fold right (higher order fn.. coming to that in the book, so leave for now)

fact2 n = foldr (*) 1 [1..n]
as = fact2 4


-- DG 2 - Fibonacci

-- Each new term in the Fibonacci sequence is generated by adding the previous two terms. 

-- By starting with 1 and 2, the first 10 terms will be:

-- 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...


-- write a function to get first 10 fibs


--[1, 2, 3, 5, 8, 13, 21, 34, 55, 89]

--at = fibs 10


-- keep generating fibs.  No base case for recursion

fibs a b =
    --if a > 89

        -- base case of the recursion.. stop at max (eg 89)..return empty list

        --  then [] 

        -- cons operator add a to start of list

        --else a : fibs b (a+b) 

        a : fibs b (a+b)

-- finding the 10,000th fib

at = last (take 10000 (fibs 1 2))
au = (fibs 1 2)!!10000
fibs' n = (fibs 1 2)!!n

-- nice way to test fibs', by throwing a range at it

av = [fibs' x | x <- [1..30]]

-- lazy

fibs'' = 1 : 1 : [x + y | (x,y) <- zip fibs'' (tail fibs'')]

-- zipWith adds 2 lists together

fibs3 = 1 : 1 : zipWith (+) fibs3 (tail fibs3)

Evolution of a Haskell coder